AES - Qabaqcıl Şifrləmə Standartı
AES simmetrik şifrləmə alqoritmidir, yəni həm şifrləmə, həm də deşifrləmə üçün eyni açardan istifadə edir.
O, TLS kimi bir çox protokolda istifadə olunur. Bu məqaləni oxuyarkən, AES, çox güman ki, bu veb-sayt ilə cihazınız arasında olan məlumatları şifrələyir.
AES 16 baytdan ibarət 4×4 matris üzərində işləyən SP-şəbəkəsidir, bu matris “vəziyyət” (state) adlanır.
Alqoritm bir neçə raunddan ibarətdir. Bir raund dörd vəziyyət transformasiyasından ibarətdir, hər bir addım yaxşı şifrləmə alqoritminin adətən malik olduğu qarışıqlıq və yayılma xüsusiyyətlərini təmin etmək üçün nəzərdə tutulub.
| AES Açar Ölçüsü | Raundlar |
|---|---|
| 128-bit | 10 |
| 192-bit | 12 |
| 256-bit | 14 |
Gəlin şifrləmə və deşifrləmənin icmalına baxaq, sonra hər bir proseduru daha ətraflı müzakirə edəcəyəm.
Şifrləmə
AES şifrləmə prosesi açar genişləndirilməsi ilə başlayır; əsas şifrləmə açarından bir neçə raund açarı əldə edilir. Bundan sonra biz sadəcə bir neçə əməliyyatdan ibarət raundları həyata keçiririk: SubBytes, ShiftRows, MixColumns və AddRoundKey.
Bu diaqrama baxın:
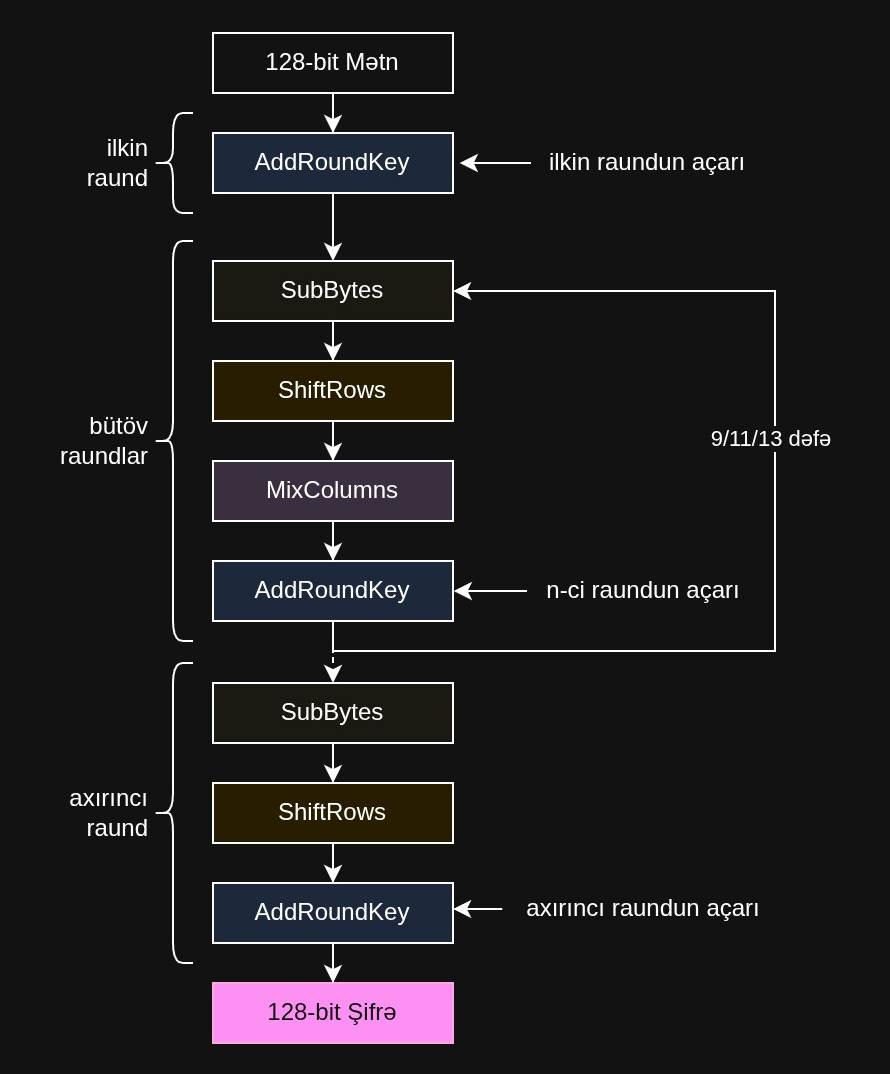
Deşifrləmə
Deşifrləmə üçün, demək olar ki, proses eynidir, lakin tərs qaydada; əməliyyatların tərs versiyalarından istifadə edirik: InvSubBytes, InvShiftRows, InvMixColumns və AddRoundKey.
Qeyd edək ki, deşifrləmədə AddRoundKey InvMixColumns-dan əvvəl gəlir ki, riyazi xüsusiyyətlər saxlanılsın.
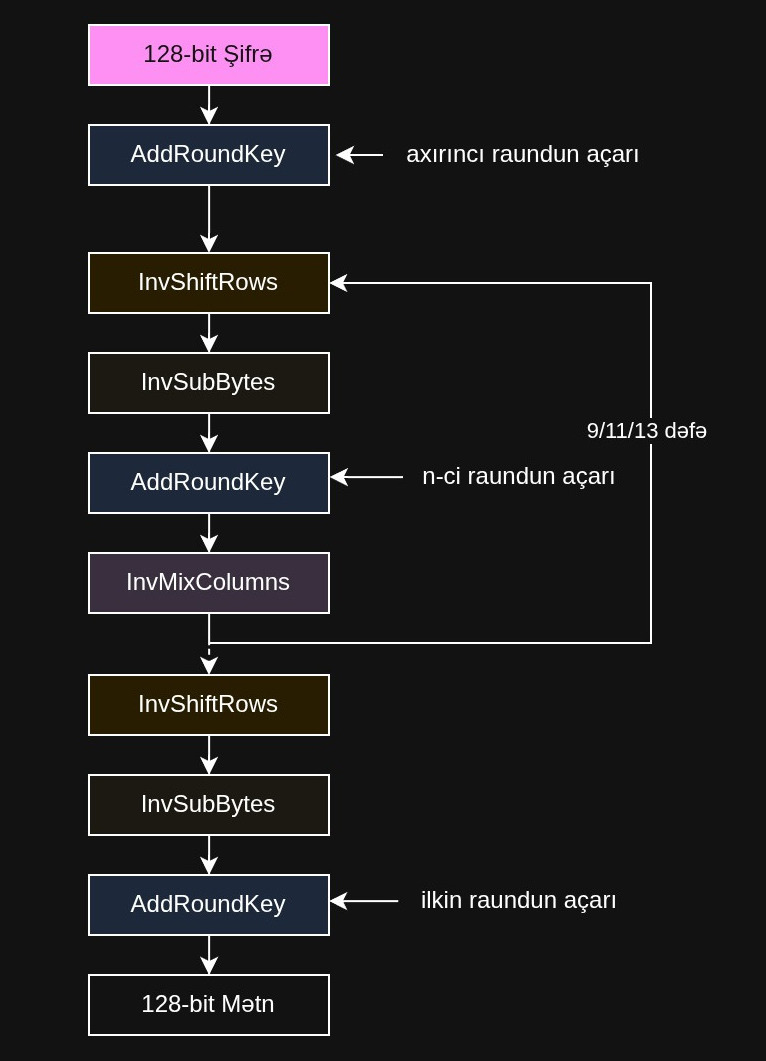
İndi hər bir proseduru daha ətraflı nəzərdən keçirək.
Açar Genişlənməsi
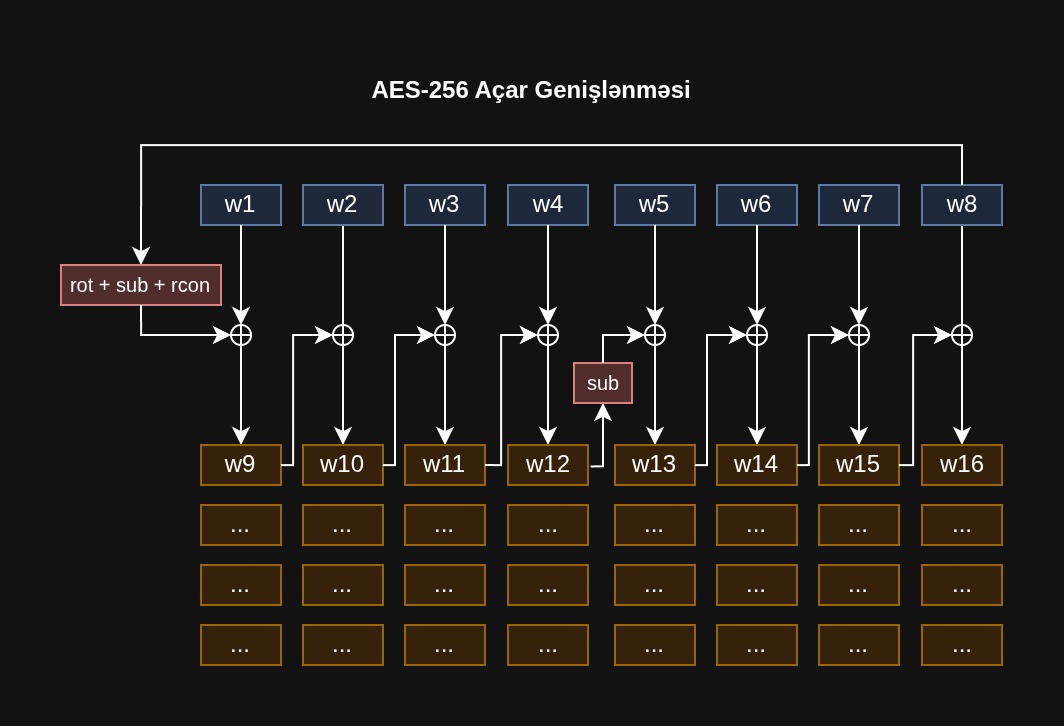
Hər şeydən əvvəl raund açarlarına ehtiyacımız var. Onlar “AES Key Schedule” adlanan xüsusi alqoritmdən istifadə edərək əsas şifrləmə açarından hesablanacaq.
Biz N+1 açar yaradacayıq, burada N əsas raundların sayıdır. Məsələn, AES-256-da 14 əsas raund var; biz 15 açar yaradacağıq, çünki ilkin raund üçün əlavə bir açara ehtiyac var.
Əsas açarımızı sözlərə bölürük. Bu kontekstdə bir söz 4 baytdır. Beləliklə, bir raund açarı 4 sözdür və ölçüsü 16 baytdır.
İlkin sözlər sadəcə əsas şifrləmə açarının sözləridir.
Yeni sözlər əvvəlki sözlərlə XOR əməliyyatlarının kombinasiyası ilə hesablanır, mövqeyə görə onlara xüsusi transformasiyalar edilə bilər.
Hər N-ci sözü (burada N əsas açarın söz uzunluğudur) generasiya edərkən baytları bir mövqe sola fırladırıq (RotWord), sonra onları sbox ilə əvəz edirik (SubWord) və nəticə xüsusi raund sabiti ilə XOR edirik.
Raund sabitləri
| Raund | Raund sabiti (RCON) |
|---|---|
| 1 | 0x01 |
| 2 | 0x02 |
| 3 | 0x04 |
| 4 | 0x08 |
| 5 | 0x10 |
| 6 | 0x20 |
| 7 | 0x40 |
| 8 | 0x80 |
| 9 | 0x1B |
| 10 | 0x36 |
| 11 | 0x6C |
| 12 | 0xD8 |
| 13 | 0xAB |
| 14 | 0x4D |
| 15 | 0x9A |
AES-256 üçün hər genişləndirmə dövrünün yarısında əlavə SubWord əməliyyatını icra etməliyik.
Bu proses bütün raund açarlarını hesablayana qədər davam edir.
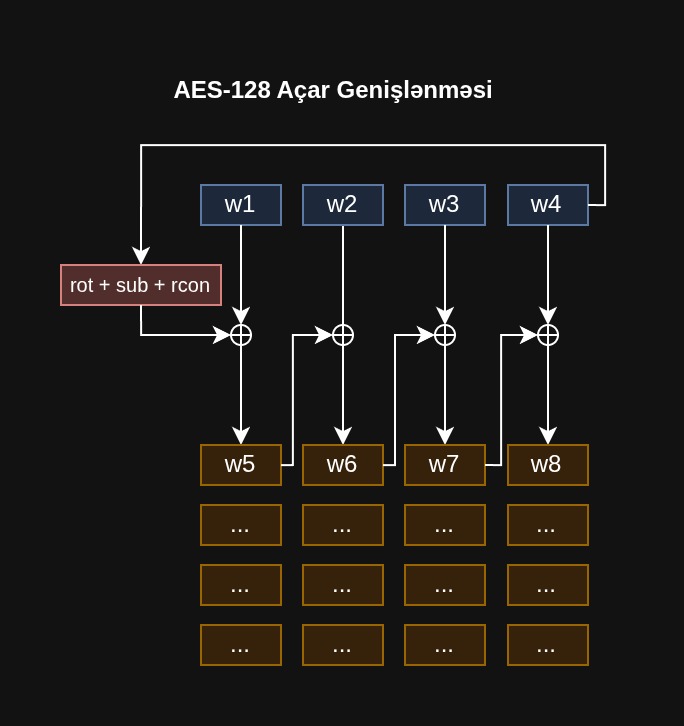
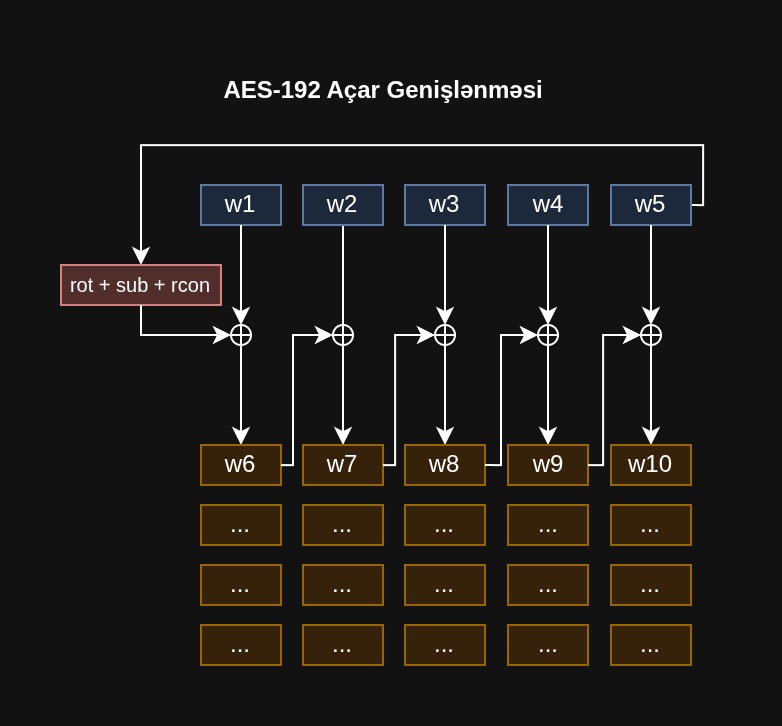
Aşağıda hər açar ölçüsü üçün açar generasiya alqoritminin necə işlədiyinə dair vizual izahatlar verilmişdir. Bəzən şəkillərlə izah etmək sözlərdən daha asandır.
AES-128 Açar Genişlənməsi
AES-192 Açar Genişlənməsi
AES-256 Açar Genişlənməsi
Açar genişləndirildikdən sonra SubBytes ilə başlayaraq əsas çevrilmələrə keçirik.
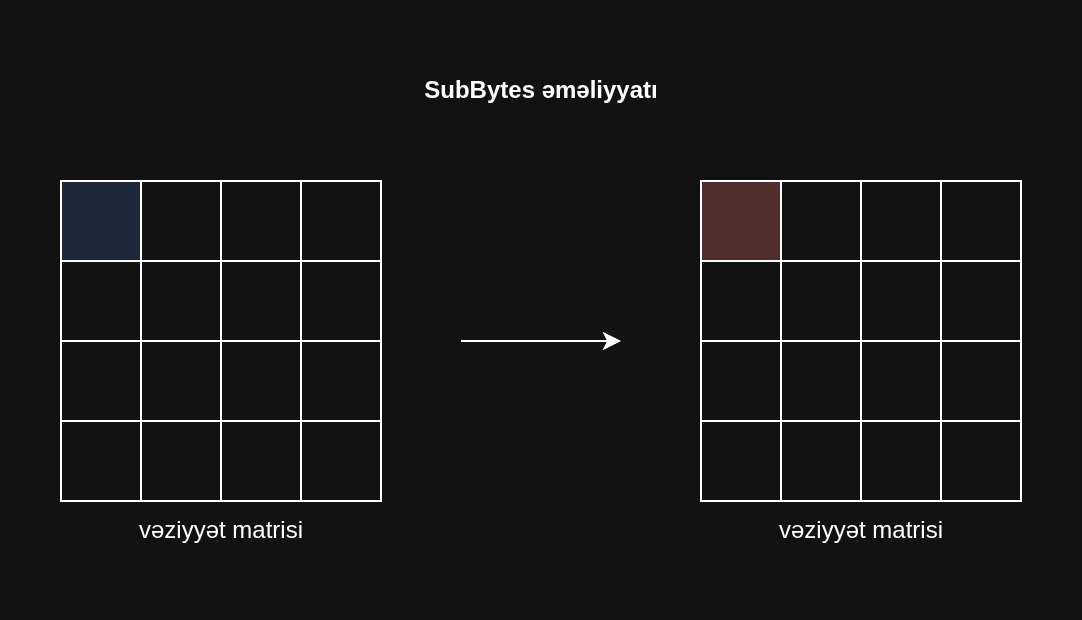
SubBytes
Bu, qeyri-xətti əvəzetmə addımıdır, burada hər bayt S-box adlanan əvvəlcədən müəyyən edilmiş cədvəldən istifadə edərək başqa bir baytla əvəz olunur.
S-box cədvəlində 256 unikal dəyər var. Bunlar bir baytın ala biləcəyi bütün mümkün dəyərlərdir.
S-box cədvəli
| Mətn baytı | Əvəzedici bayt |
|---|---|
| 00000000 | 01100011 |
| 00000001 | 01111100 |
| 00000010 | 01110111 |
| 00000011 | 01111011 |
| 00000100 | 11110010 |
| 00000101 | 01101011 |
| 00000110 | 01101111 |
| 00000111 | 11000101 |
| 00001000 | 00110000 |
| 00001001 | 00000001 |
| 00001010 | 01100111 |
| 00001011 | 00101011 |
| 00001100 | 11111110 |
| 00001101 | 11010111 |
| 00001110 | 10101011 |
| 00001111 | 01110110 |
| 00010000 | 11001010 |
| 00010001 | 10000010 |
| 00010010 | 11001001 |
| 00010011 | 01111101 |
| 00010100 | 11111010 |
| 00010101 | 01011001 |
| 00010110 | 01000111 |
| 00010111 | 11110000 |
| 00011000 | 10101101 |
| 00011001 | 11010100 |
| 00011010 | 10100010 |
| 00011011 | 10101111 |
| 00011100 | 10011100 |
| 00011101 | 10100100 |
| 00011110 | 01110010 |
| 00011111 | 11000000 |
| 00100000 | 10110111 |
| 00100001 | 11111101 |
| 00100010 | 10010011 |
| 00100011 | 00100110 |
| 00100100 | 00110110 |
| 00100101 | 00111111 |
| 00100110 | 11110111 |
| 00100111 | 11001100 |
| 00101000 | 00110100 |
| 00101001 | 10100101 |
| 00101010 | 11100101 |
| 00101011 | 11110001 |
| 00101100 | 01110001 |
| 00101101 | 11011000 |
| 00101110 | 00110001 |
| 00101111 | 00010101 |
| 00110000 | 00000100 |
| 00110001 | 11000111 |
| 00110010 | 00100011 |
| 00110011 | 11000011 |
| 00110100 | 00011000 |
| 00110101 | 10010110 |
| 00110110 | 00000101 |
| 00110111 | 10011010 |
| 00111000 | 00000111 |
| 00111001 | 00010010 |
| 00111010 | 10000000 |
| 00111011 | 11100010 |
| 00111100 | 11101011 |
| 00111101 | 00100111 |
| 00111110 | 10110010 |
| 00111111 | 01110101 |
| 01000000 | 00001001 |
| 01000001 | 10000011 |
| 01000010 | 00101100 |
| 01000011 | 00011010 |
| 01000100 | 00011011 |
| 01000101 | 01101110 |
| 01000110 | 01011010 |
| 01000111 | 10100000 |
| 01001000 | 01010010 |
| 01001001 | 00111011 |
| 01001010 | 11010110 |
| 01001011 | 10110011 |
| 01001100 | 00101001 |
| 01001101 | 11100011 |
| 01001110 | 00101111 |
| 01001111 | 10000100 |
| 01010000 | 01010011 |
| 01010001 | 11010001 |
| 01010010 | 00000000 |
| 01010011 | 11101101 |
| 01010100 | 00100000 |
| 01010101 | 11111100 |
| 01010110 | 10110001 |
| 01010111 | 01011011 |
| 01011000 | 01101010 |
| 01011001 | 11001011 |
| 01011010 | 10111110 |
| 01011011 | 00111001 |
| 01011100 | 01001010 |
| 01011101 | 01001100 |
| 01011110 | 01011000 |
| 01011111 | 11001111 |
| 01100000 | 11010000 |
| 01100001 | 11101111 |
| 01100010 | 10101010 |
| 01100011 | 11111011 |
| 01100100 | 01000011 |
| 01100101 | 01001101 |
| 01100110 | 00110011 |
| 01100111 | 10000101 |
| 01101000 | 01000101 |
| 01101001 | 11111001 |
| 01101010 | 00000010 |
| 01101011 | 01111111 |
| 01101100 | 01010000 |
| 01101101 | 00111100 |
| 01101110 | 10011111 |
| 01101111 | 10101000 |
| 01110000 | 01010001 |
| 01110001 | 10100011 |
| 01110010 | 01000000 |
| 01110011 | 10001111 |
| 01110100 | 10010010 |
| 01110101 | 10011101 |
| 01110110 | 00111000 |
| 01110111 | 11110101 |
| 01111000 | 10111100 |
| 01111001 | 10110110 |
| 01111010 | 11011010 |
| 01111011 | 00100001 |
| 01111100 | 00010000 |
| 01111101 | 11111111 |
| 01111110 | 11110011 |
| 01111111 | 11010010 |
| 10000000 | 11001101 |
| 10000001 | 00001100 |
| 10000010 | 00010011 |
| 10000011 | 11101100 |
| 10000100 | 01011111 |
| 10000101 | 10010111 |
| 10000110 | 01000100 |
| 10000111 | 00010111 |
| 10001000 | 11000100 |
| 10001001 | 10100111 |
| 10001010 | 01111110 |
| 10001011 | 00111101 |
| 10001100 | 01100100 |
| 10001101 | 01011101 |
| 10001110 | 00011001 |
| 10001111 | 01110011 |
| 10010000 | 01100000 |
| 10010001 | 10000001 |
| 10010010 | 01001111 |
| 10010011 | 11011100 |
| 10010100 | 00100010 |
| 10010101 | 00101010 |
| 10010110 | 10010000 |
| 10010111 | 10001000 |
| 10011000 | 01000110 |
| 10011001 | 11101110 |
| 10011010 | 10111000 |
| 10011011 | 00010100 |
| 10011100 | 11011110 |
| 10011101 | 01011110 |
| 10011110 | 00001011 |
| 10011111 | 11011011 |
| 10100000 | 11100000 |
| 10100001 | 00110010 |
| 10100010 | 00111010 |
| 10100011 | 00001010 |
| 10100100 | 01001001 |
| 10100101 | 00000110 |
| 10100110 | 00100100 |
| 10100111 | 01011100 |
| 10101000 | 11000010 |
| 10101001 | 11010011 |
| 10101010 | 10101100 |
| 10101011 | 01100010 |
| 10101100 | 10010001 |
| 10101101 | 10010101 |
| 10101110 | 11100100 |
| 10101111 | 01111001 |
| 10110000 | 11100111 |
| 10110001 | 11001000 |
| 10110010 | 00110111 |
| 10110011 | 01101101 |
| 10110100 | 10001101 |
| 10110101 | 11010101 |
| 10110110 | 01001110 |
| 10110111 | 10101001 |
| 10111000 | 01101100 |
| 10111001 | 01010110 |
| 10111010 | 11110100 |
| 10111011 | 11101010 |
| 10111100 | 01100101 |
| 10111101 | 01111010 |
| 10111110 | 10101110 |
| 10111111 | 00001000 |
| 11000000 | 10111010 |
| 11000001 | 01111000 |
| 11000010 | 00100101 |
| 11000011 | 00101110 |
| 11000100 | 00011100 |
| 11000101 | 10100110 |
| 11000110 | 10110100 |
| 11000111 | 11000110 |
| 11001000 | 11101000 |
| 11001001 | 11011101 |
| 11001010 | 01110100 |
| 11001011 | 00011111 |
| 11001100 | 01001011 |
| 11001101 | 10111101 |
| 11001110 | 10001011 |
| 11001111 | 10001010 |
| 11010000 | 01110000 |
| 11010001 | 00111110 |
| 11010010 | 10110101 |
| 11010011 | 01100110 |
| 11010100 | 01001000 |
| 11010101 | 00000011 |
| 11010110 | 11110110 |
| 11010111 | 00001110 |
| 11011000 | 01100001 |
| 11011001 | 00110101 |
| 11011010 | 01010111 |
| 11011011 | 10111001 |
| 11011100 | 10000110 |
| 11011101 | 11000001 |
| 11011110 | 00011101 |
| 11011111 | 10011110 |
| 11100000 | 11100001 |
| 11100001 | 11111000 |
| 11100010 | 10011000 |
| 11100011 | 00010001 |
| 11100100 | 01101001 |
| 11100101 | 11011001 |
| 11100110 | 10001110 |
| 11100111 | 10010100 |
| 11101000 | 10011011 |
| 11101001 | 00011110 |
| 11101010 | 10000111 |
| 11101011 | 11101001 |
| 11101100 | 11001110 |
| 11101101 | 01010101 |
| 11101110 | 00101000 |
| 11101111 | 11011111 |
| 11110000 | 10001100 |
| 11110001 | 10100001 |
| 11110010 | 10001001 |
| 11110011 | 00001101 |
| 11110100 | 10111111 |
| 11110101 | 11100110 |
| 11110110 | 01000010 |
| 11110111 | 01101000 |
| 11111000 | 01000001 |
| 11111001 | 10011001 |
| 11111010 | 00101101 |
| 11111011 | 00001111 |
| 11111100 | 10110000 |
| 11111101 | 01010100 |
| 11111110 | 10111011 |
| 11111111 | 00010110 |
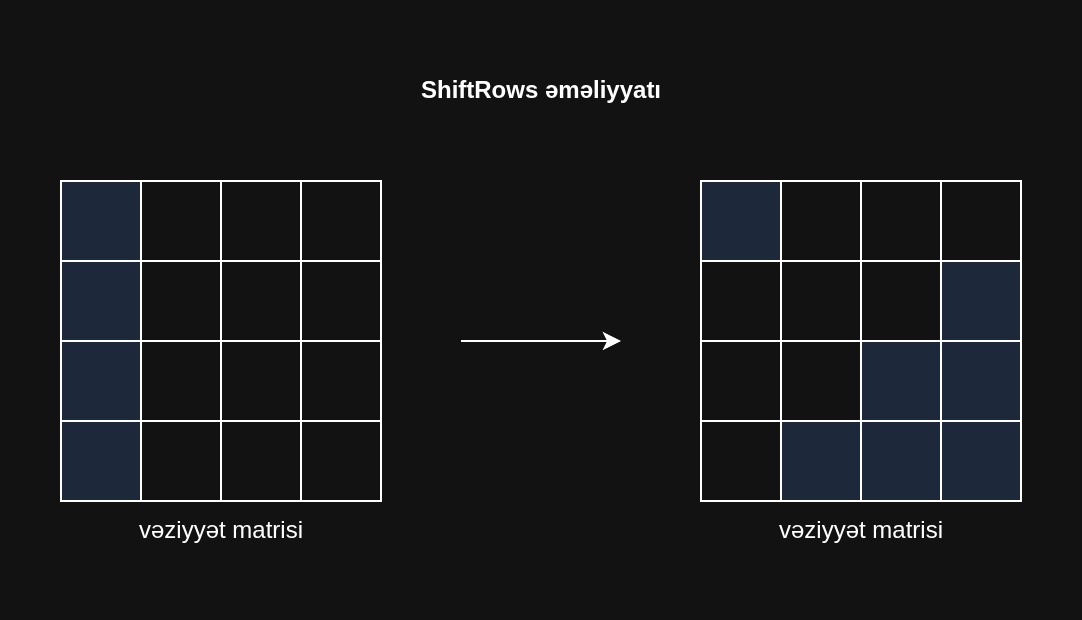
ShiftRows
ShiftRows addımında hər sətir dairəvi şəkildə sola çəkilir:
- Sətir 1: yerində qalır
- Sətir 2: 1 bayt sola çəkilir
- Sətir 3: 2 bayt sola çəkilir
- Sətir 4: 3 bayt sola çəkilir
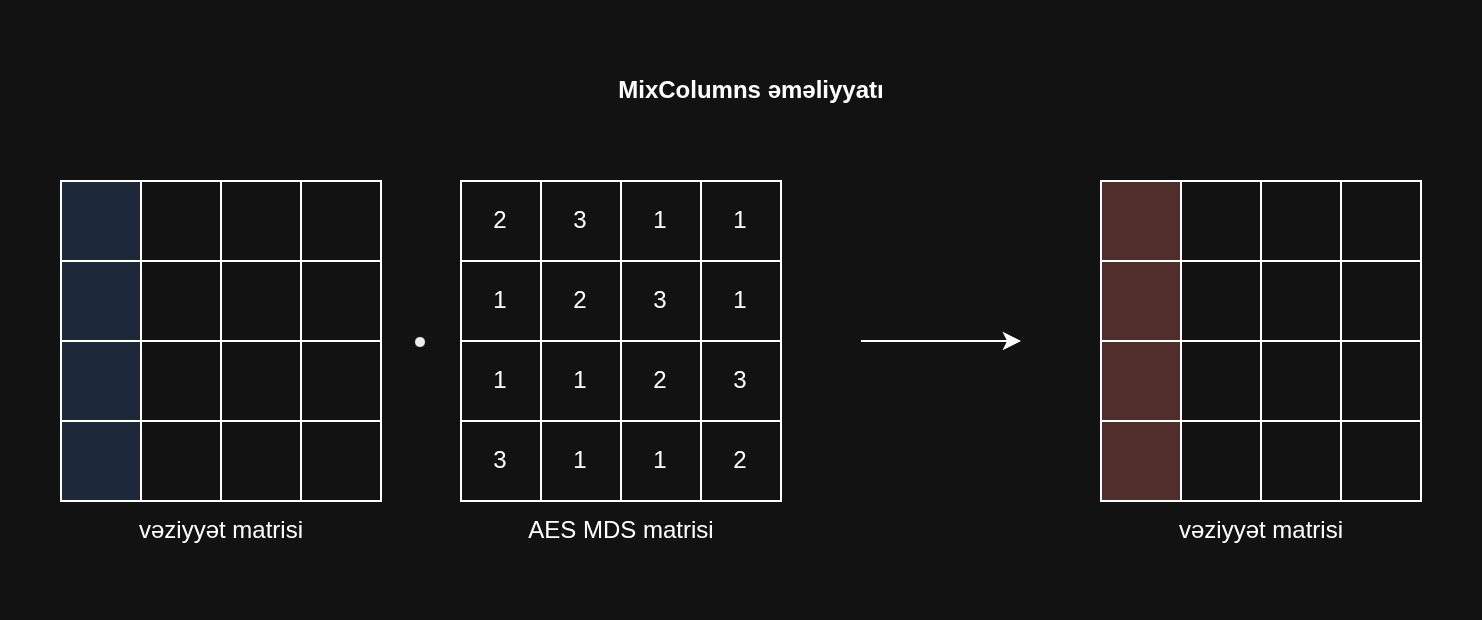
MixColumns
MixColumns addımında hər sütun Galois Sahəsi GF(2⁸) üzərində sabit 4x4 matrisinə vurulur.
Bu vurma standart skalyar hasil deyil, lakin oxşar bir əməliyyatdır.
Hər baytı aşağıdakı polinom kimi təsvir edirik:
b7·x^7 + b6·x^6 + b5·x^5 + b4·x^4 + b3·x^3 + b2·x^2 + b1·x + b0
Matris vurması zamanı “toplama” XOR ilə həyata keçirilir, “vurma” isə polinom vurmasını və x⁸+x⁴+x³+x+1 polinomu ilə modul azaldılmasını əhatə edir.
Bu əməliyyat yayılmanı həyata keçirir, burada hər bayt eyni sütundakı bütün digər baytlardan asılı bir dəyər alır, bu da şifrəmətni statistik təhlilini çətinləşdirir.
Qeyd: Son raundda deşifrləməni asanlaşdırmaq və əlavə hesablamalardan uzaq olmaq üçün MixColumns addımını icra etmirik.
AddRoundKey
Bu addımda vəziyyətin hər baytı raund açarının müvafiq baytı ilə XOR əməliyyatı istifadə edərək matris kombinə olunur.
Yeri gəlmişkən, deşifrləmə üçün ayrıca InvAddRoundKey addımına ehtiyac yoxdur, çünki ikinci XOR tətbiqi birincisini onsuzda ləğv edir.

Əməliyyat Rejimləri
Bir bloku rejimsiz şifrləmək mümükündür, lakin bir neçə blok olanda biz adətən ECB, CBC, CTR və GCM kimi əməliyyat rejimlərindən istifadə edirik. Bu rejimlər şifrləmənin bir neçə blok üzərində tətbiqini müəyyənləşdirir.
| Rejim | Təsvir |
|---|---|
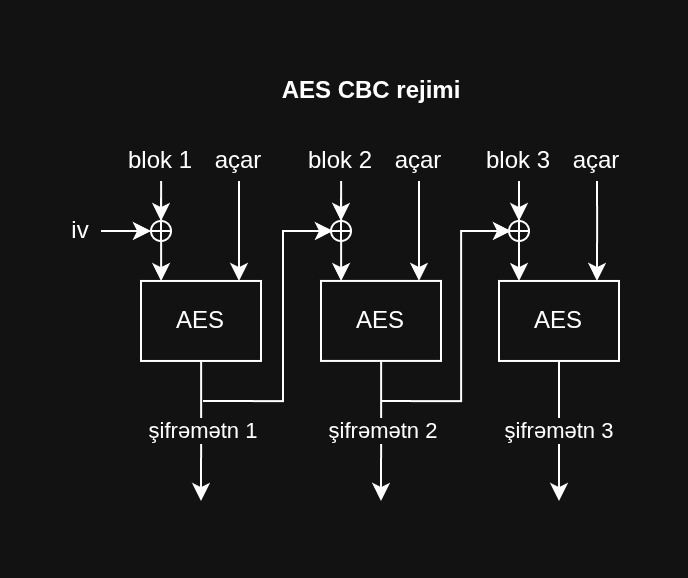
| ECB | Hər blok müstəqil şəkildə şifrələnir. |
| CBC | Hər blok əvvəlki şifrəli mətnlə qarışdırılır. |
| CTR | Sayğac dəyəri şifrələnir və blokla qarışdırılır. |
| GCM | CTR rejimi kimi + əlavə bütövlüyü yoxlaması imkanı. |
CBC rejiminin vizual nümunəsi:
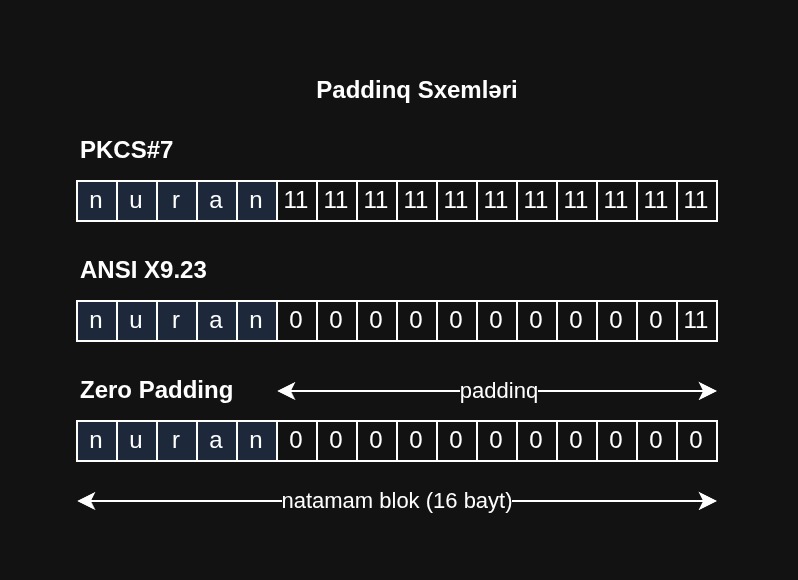
Paddinq Sxemləri
Mətn çox vaxt AES-in 16 bayt olan blok ölçüsünə tam bölünmür; boş yer qalır.
Qalan yeri doldurmaq üçün paddinq sxemləri (doldurma sxemləri) istifadə olunur. Tanınmış paddinq sxemləri PKCS#7, ANSI X.923 və Zero Padding.
PKCS#7 bloku tamamlamaq üçün N bayt dəyərini N dəfə boş yerlərə əlavə edir. Məlumat 16 bayta tam uyğun gəlsə belə, əlavə tam paddinq bloku əlavə edir.
ANSI X.923 son paddinq baytını paddinq uzunluğuna təyin edir və qalanını sıfırlarla doldurur. PKCS#7 kimi, paddinq tələb olunmadıqda belə əlavə paddinq bloku əlavə edir.
Zero Padding boş yeri sadəcə sıfırlarla doldurur, baxmayaraq ki, bu, açıq mətn təbii olaraq sıfırlarla bitərsə problemlər yarada bilər.
Açar Mübadiləsi Problemi
Simmetrik şifrləmə sistemlərinin ümumi problemi olan açar mübadiləsi məsələsidir. Hər iki tərəf eyni gizli açara malik olmalıdır. Ən təhlükəsiz yol açarı ikinci tərəflə şəxsi görüşdə təqdim etmək ola bilər, lakin bu uzaq məsafələr üçün praktiki deyil. Diffie-Hellman açar mübadiləsi riyaziyyatdan istifadə edərək iki tərəfin açıq kanal üzərindən ümumi gizli açar yaratmasına imkan verir (bu barədə ayrıca məqalə yazmışam).
Performans
AES standart olaraq seçilməsinin səbəbi təkcə yaxşı şifrləmə performansı deyil, həm də bunu çox sürətli etməsidir.
Intel və AMD hətta AES şifrləməsi üçün birbaşa CPU təlimatları tətbiq etmişdir.
Həmçinin, MixColumns addımında polinom vurmasını hər dəfə həyata keçirmək əvəzinə, bütün mümkün bayt dəyərləri üçün nəticələr əvvəlcədən hesablana və cədvəldən tapıla bilər. Cədvəlin giriş vaxtı adətən O(1)-dir, yəni sabit bir vaxtdır.
Qabaqcıl Şifrləmə Standartı haqqında bu məqaləni oxuduğunuz üçün təşəkkür edirəm. Sizə xoş gün arzulayıram.
C dilində yazdığım AES-256-CBC alqoritminin implementasiyasını bu repozitoriyadan oxuya bilərsiniz.